Lamport clocks algorithm
Lamport clocks in words
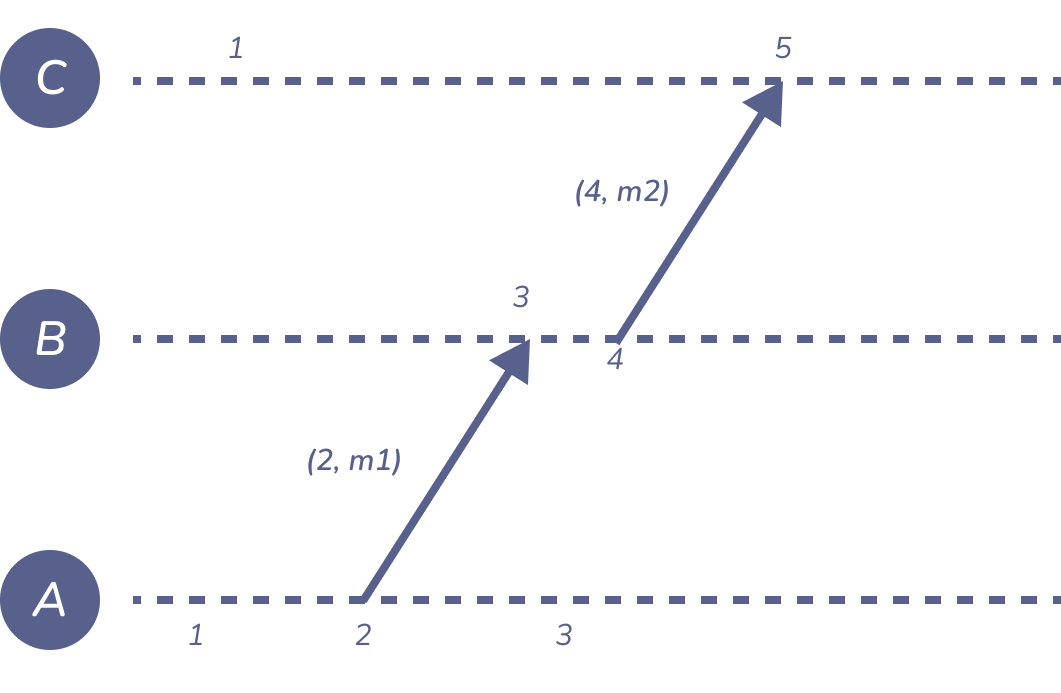
Figure 1: lamport-example-simple
- 每个节点都维护一个计数器 \(t\),每一个当前节点事件 \(e\) 发生时,自增 1。
- 增长后的值设为 \(L(e)\)
- 发送消息时附带上当前的计数 \(t\)
- 消息接受者在消息中的时间戳和当前节点的时间戳之间取最大值后自增 1
Properties of this scheme:
- if \(a \rightarrow b\) then \(L(e) < L(b)\)
- However, \(L(a) < L(b)\) does not imply \(a \rightarrow b\)
- Possible that \(L(a) = L(b)\) for \(a \ne b\)
Lamport 时间戳本质上是一个整数,用来计算已发生事件的数量。因此,它与物理时间没有直接关系。在每个节点上,时间都会增加,因为每个事件的整数都会递增。该算法假设了一个 crash-stop 模型(如果时间戳被保持在稳定的存储中,即在磁盘上,则是 crash-recovery 模型)。
Lamport clocks example
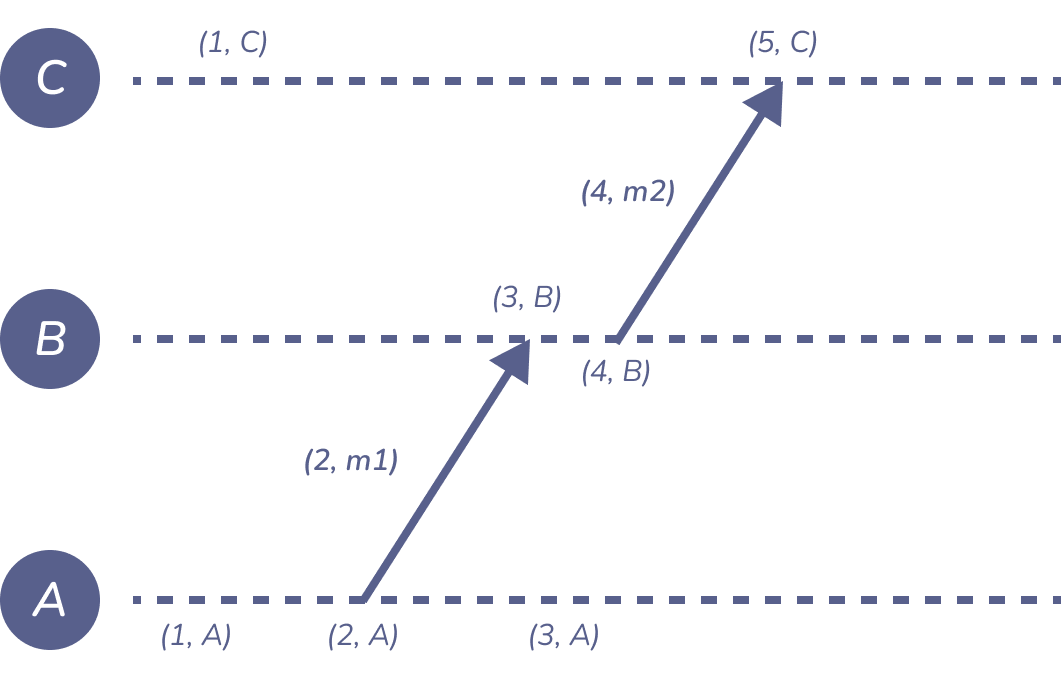
Figure 2: lamport-example
Let \(N(e)\) be the node at which event \(e\) occurred.
Then the pair \((L(e), N(e))\) uniquely identifies event \(e\).
Define a total order \(\prec\) using Lamport timestamps:
\((a \prec b) \iff (L(a) < L(b) \vee (L(a) = L(b) \wedge N(a) < N(b)))\)1 , 2
This order is causal: \((a \rightarrow b) \longrightarrow (a \prec b)\)
回顾之前的 happens-before relation 是局部顺序。利用 Lamport 时间戳可以将这种局部的顺序扩展到全局顺序。可以用(时间戳, 节点名称) 组合:首先比较时间戳,如果相同,则比较节点名称。
对于任何两个事件 \(a \ne b\),那么既不是 \(a \prec b\) 也不是 \(b \prec a\)。只要 \(a \rightarrow b\),我们就有 \(a \prec b\),换句话说,\(\prec\) 是局部顺序 \(\rightarrow\) 的线性扩展。然而,如果 \(a \vert \vert b\),我们可以有 \(a \prec b\) 或 \(b \prec a\),所以两个事件的顺序是由算法任意决定的。 比如 \((1, A)\) 和 \((1, C)\) 两个事件是平行的,按照 Lamport 的算法,\((1, A)\) 必然是在 \((1, C)\) 之前的,但实际情况可能是 \((1, C)\) 在前。