给定的 Lamport 时间戳 \(L(a)\) 和 \(L(b)\) 并且 \(L(a) < L(b)\),我们推断不出 \(a \rightarrow b\) 或者 \(a || b\).1
要区分平行的这些事件,需要 vertor clocks:
- 假定分布式系统中有 \(n\) 个节点,\(N = \langle N_{1}, N_{2},…, N_{n}\rangle\)
- 事件 \(a\) 的向量时间戳写成 \(V(a) = \langle t_{1}, t_{2},…, t_{n} \rangle\)
- \(t_{i}\) 是 \(N_{i}\) 节点发生时间的数量
- 每个节点都有一个当前的向量时间戳 \(T\)
- 节点 \(N_{i}\) 上的事件,向量时间戳 \(T[i]\) 递增。
- 每个消息都附带上向量时间戳
- 接收者将消息中的向量时间戳合并到本地
除了标量和向量之间的区别之外,向量时钟算法与 Lamport 时钟非常相似。一个节点的向量时钟的初始值是系统中的每个节点的事件数,也就是 0。每当节点 \(N_{i}\) 发生事件时,它就会增加其向量钟中的第 \(i\) 个条目(它自己的条目)。(In practice, this vector is often implemented as a map from node IDs to integers rather than an array of integers. 在实践中,这里的向量通常是节点 ID 对应 Integer 的 map,而不是 Integer 的数组。)。当一个消息在网络上被发送时,发送者当前的向量时间戳被附加到该消息上。最后,当一个消息被接收时,接收者将消息中的向量时间戳与它的本地时间戳合并,方法是取两个向量的元素的最大值,然后接收者增加它自己的条目。
Vector clocks algorithm
Vector clocks example
假定节点向量是 \(N = \langle A, B, C \rangle\):
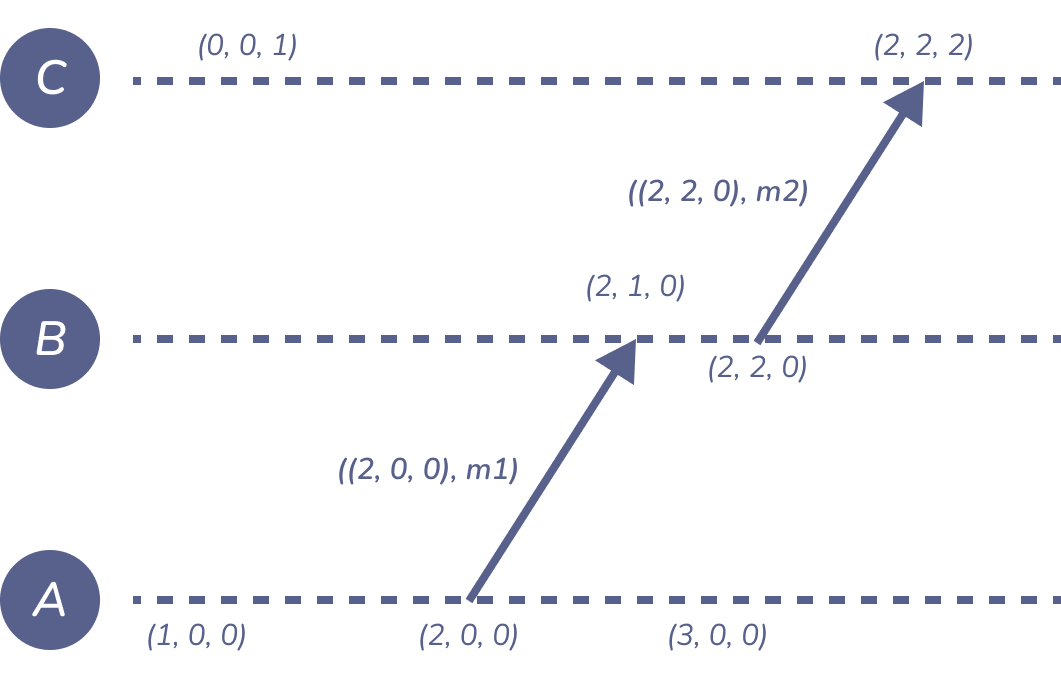
Figure 1: vector-example
事件 \(e\) 的向量时间戳是一系列事件的集合, \(e\) 和它的因果以来:\({e} \cup {a | a \rightarrow e}\)23
比如,\(\langle2, 2, 0\rangle\),第一个 2 是表示来自于 \(A\) 的两个事件,第二个 2 是表示来自于 \(B\) 的两个事件,并且没有来自于 \(C\) 的事件。
Vector clocks ordering
Define the following order on vector timestamps(in a system with \(n\) nodes):
- \(T = T’ \iff T[i] = T’[i]\) for all \(i \in {1, …, n}\)
- \(T \le T’ \iff T[i] \le T’[i]\) for all \(\in {1, …, n}\)
- \(T < T’ \iff T \le T’\) and \(T \neq T’\)
- \(T || T’ \iff T > T’\) and \(T’ > T\)
\(V(a) \le V(b) \iff ({a} \cup {e | e \rightarrow a}) \subseteq ({b} \cup{} {e | e \rightarrow b})\)
Properties of this order:
- \((V(a) < V(b)) \iff (a \rightarrow b)\)
- \((V(a) = V(b)) \iff (a = b)\)
- \((V(a) \rVert V(b)) \iff (a \rVert b)\)
然后,我们对向量的时间戳进行部分排序。如果第一个向量的每个元素都小于或等于第二个向量的相应元素,我们就说一个向量小于或等于另一个向量。如果一个向量小于或等于另一个向量,并且它们至少有一个元素是不同的,那么这个向量就严格小于另一个向量。然而,如果一个向量在一个元素中的值较大,而另一个向量在另一个元素中的值较大,那么这两个向量是不可比的。例如,\(T = \langle2, 2, 0\rangle\) 和 \(T’ = \langle0, 0, 1\rangle\) 是不可比的,因为 \(T[1] > T’[1]\) 但 \(T[3] < T’[3]\)。
向量时间戳的部分顺序与发生之前关系所定义的部分顺序完全对应。因此,向量时钟算法为我们提供了一种在实践中计算发生前关系的机制。
-
具体参考 Lamport Clocks 中的逻辑双条件。 ↩︎
-
\(\cup\) 并集的意思,\(\cap\) 交集的意思。 ↩︎
-
集合的描述方法,描述格式为 \({x | P(x), x \in \Omega}\)。 ↩︎